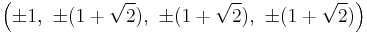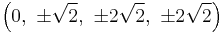Truncated tesseract

Tesseract	Truncated tesseract	Rectified tesseract	Bitruncated tesseract
Schlegel diagrams centered on [4,3] (cells visible at [3,3])
16-cell	Truncated 16-cell	Rectified 16-cell (24-cell)	Bitruncated tesseract
Schlegel diagrams centered on [3,3] (cells visible at [4,3])

In geometry, a truncated tesseract is a uniform polychoron (4-dimensional uniform polytope) formed as the truncation of the regular tesseract.

There are three trunctions, including a bitruncation, and a tritruncation, which creates the truncated 16-cell.

Truncated tesseract

Trucated tesseract
Schlegel diagram (tetrahedron cells visible)
Type	Uniform polychoron
Schläfli symbol	t_0,1{4,3,3}
Coxeter-Dynkin diagrams
Cells	24	8 3.8.8 16 3.3.3
Faces	88	64 {3} 24 {8}
Edges	128
Vertices	64
Vertex figure	Isosceles triangular pyramid
Dual	Tetrakis 16-cell
Symmetry group	A₄, [4,3,3]
Properties	convex
Uniform index	12 13 14

The truncated tesseract is bounded by 24 cells: 8 truncated cubes, and 16 tetrahedra.

Alternate names

Truncated tesseract (Norman W. Johnson)
Truncated tesseract (Acronym tat) (George Olshevsky, and Jonathan Bowers)^[1]

Construction

The truncated tesseract may be constructed by truncating the vertices of the tesseract at 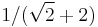$1/(\sqrt{2}%2B2)$ of the edge length. A regular tetrahedron is formed at each truncated vertex.

The Cartesian coordinates of the vertices of a truncated tesseract having edge length 2 is given by all permutations of:

$\left(\pm1,\ \pm(1%2B\sqrt{2}),\ \pm(1%2B\sqrt{2}),\ \pm(1%2B\sqrt{2})\right)$

Projections

In the truncated cube first parallel projection of the truncated tesseract into 3-dimensional space, the image is laid out as follows:

The projection envelope is a cube.
Two of the truncated cube cells project onto a truncated cube inscribed in the cubical envelope.
The other 6 truncated cubes project onto the square faces of the envelope.
The 8 tetrahedral volumes between the envelope and the triangular faces of the central truncated cube are the images of the 16 tetrahedra, a pair of cells to each image.

Images

orthographic projections
Coxeter plane	B₄	B₃ / D₄ / A₂	B₂ / D₃
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	F₄	A₃
Graph
Dihedral symmetry	[12/3]	[4]

A polyhedral net	Truncated tesseract projected onto the 3-sphere with a stereographic projection into 3-space.

Bitruncated tesseract

Bitruncated tesseract
Two Schlegel diagrams, centered on truncated tetrahedral or truncated octahedral cells, with alternate cell types hidden.
Type	Uniform polychoron
Schläfli symbol	t_1,2{4,3,3} t_0,1,2{3^1,1,1}
Coxeter-Dynkin diagrams
Cells	24	8 4.6.6 16 3.6.6
Faces	120	32 {3} 24 {4} 64 {6}
Edges	192
Vertices	96
Vertex figure	Digonal disphenoid
Symmetry group	B₄, [3,3,4] D₄, [3^1,1,1]
Properties	convex, vertex-transitive
Uniform index	15 16 17

The bitruncated tesseract (also called a bitruncated 16-cell) is constructed by a bitruncation operation applied to the tesseract.

Alternate names

Bitruncated tesseract (Norman W. Johnson)
Bitruncated tesseract (Acronym tah) (George Olshevsky, and Jonathan Bowers)^[2]

Construction

A tesseract is bitruncated by truncating its cells beyond their mid-points, turning the eight cubes into eight truncated octahedra. These still share their square faces, but the hexagonal faces form truncated tetrahedra which share their triangular faces with each other.

The Cartesian coordinates of the vertices of a bitruncated tesseract having edge length 2 is given by all permutations of:

$\left(0,\ \pm\sqrt{2},\ \pm2\sqrt{2},\ \pm2\sqrt{2}\right)$

Structure

The truncated octahedra are connected to each other via their square faces, and to the truncated tetrahedra via their hexagonal faces. The truncated tetrahedra are connected to each other via their triangular faces.

Projections

orthographic projections
Coxeter plane	B₄	B₃ / D₄ / A₂	B₂ / D₃
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	F₄	A₃
Graph
Dihedral symmetry	[12/3]	[4]

Stereographic projections

The truncated-octahedron-first projection of the bitruncated tesseract into 3D space has a truncated cubical envelope. Two of the truncated octahedral cells project onto a truncated octahedron inscribed in this envelope, with the square faces touching the centers of the octahedral faces. The 6 octahedral faces are the images of the remaining 6 truncated octahedral cells. The remaining gap between the inscribed truncated octahedron and the envelope are filled by 8 flattened truncated tetrahedra, each of which is the image of a pair of truncated tetrahedral cells.

Stereographic projections
	Colored transparently with pink triangles, blue squares, and gray hexagons

Truncated 16-cell

Truncated 16-cell
Schlegel diagram (octahedron cells visible)
Type	Uniform polychoron
Schläfli symbol	t_0,1{4,3,3} t_0,1{3^1,1,1}
Coxeter-Dynkin diagrams
Cells	24	8 3.3.3.3 16 3.6.6
Faces	96	64 {3} 32 {6}
Edges	120
Vertices	48
Vertex figure	square pyramid
Dual	Hexakis tesseract
Coxeter groups	BC₄ [3,3,4] D₄ [3^1,1,1]
Properties	convex
Uniform index	16 17 18

The truncated 16-cell which is bounded by 24 cells: 8 regular octahedra, and 16 truncated tetrahedra.

It is related to, but not to be confused with, the 24-cell, which is a regular polychoron bounded by 24 regular octahedra.

Alternate names

Truncated 16-cell (Norman W. Johnson)
Truncated hexadecachoron (Acronym thex) (George Olshevsky, and Jonathan Bowers)^[3]

Construction

The truncated 16-cell may be constructed from the 16-cell by truncating its vertices at 1/3 of the edge length. This results in the 16 truncated tetrahedral cells, and introduces the 8 octahedra (vertex figures).

(Truncating a 16-cell at 1/2 of the edge length results in the 24-cell, which has a greater degree of symmetry because the truncated cells become identical with the vertex figures.)

The Cartesian coordinates of the vertices of a truncated 16-cell having edge length 2√2 are given by all permutations, and sign combinations:

(0,0,1,2)

An alternate construction begins with a demitesseract with vertex coordinates (±3,±3,±3,±3), having an even number of each sign, and truncates it to obtain the permutations of

(1,1,3,3), with an even number of each sign.

Structure

The truncated tetrahedra are joined to each other via their hexagonal faces. The octahedra are joined to the truncated tetrahedra via their triangular faces.

Projections

Centered on octahedron

The octahedron-first parallel projection of the truncated 16-cell into 3-dimensional space has the following structure:

The projection envelope is a truncated octahedron.
The 6 square faces of the envelope are the images of 6 of the octahedral cells.
An octahedron lies at the center of the envelope, joined to the center of the 6 square faces by 6 edges. This is the image of the other 2 octahedral cells.
The remaining space between the envelope and the central octahedron is filled by 8 truncated tetrahedra (distorted by projection). These are the images of the 16 truncated tetrahedral cells, a pair of cells to each image.

This layout of cells in projection is analogous to the layout of faces in the projection of the truncated octahedron into 2-dimensional space. Hence, the truncated 16-cell may be thought of as the 4-dimensional analogue of the truncated octahedron.

Centered on truncated tetrahedron

The truncated tetrahedron first parallel projection of the truncated 16-cell into 3-dimensional space has the following structure:

The projection envelope is a truncated cube.
The nearest truncated tetrahedron to the 4D viewpoint projects to the center of the envelope, with its triangular faces joined to 4 octahedral volumes that connect it to 4 of the triangular faces of the envelope.
The remaining space in the envelope is filled by 4 other truncated tetrahedra.
These volumes are the images of the cells lying on the near side of the truncated 16-cell; the other cells project onto the same layout except in the dual configuration.
The six octagonal faces of the projection envelope are the images of the remaining 6 truncated tetrahedral cells.

Images

orthographic projections
Coxeter plane	B₄	B₃ / D₄ / A₂	B₂ / D₃
Graph
Dihedral symmetry	[8]	[6]	[4]
Coxeter plane	F₄	A₃
Graph
Dihedral symmetry	[12/3]	[4]

net	stereographic projection (centered on truncated tetrahedron)

Related uniform polytopes

Name	tesseract	rectified tesseract	truncated tesseract	cantellated tesseract	runcinated tesseract	bitruncated tesseract	cantitruncated tesseract	runcitruncated tesseract	omnitruncated tesseract
Coxeter-Dynkin diagram
Schläfli symbol	{4,3,3}	t₁{4,3,3}	t_0,1{4,3,3}	t_0,2{4,3,3}	t_0,3{4,3,3}	t_1,2{4,3,3}	t_0,1,2{4,3,3}	t_0,1,3{4,3,3}	t_0,1,2,3{4,3,3}
Schlegel diagram
B₄ Coxeter plane graph

Name	16-cell	rectified 16-cell	truncated 16-cell	cantellated 16-cell	runcinated 16-cell	bitruncated 16-cell	cantitruncated 16-cell	runcitruncated 16-cell	omnitruncated 16-cell
Coxeter-Dynkin diagram
Schläfli symbol	{3,3,4}	t₁{3,3,4}	t_0,1{3,3,4}	t_0,2{3,3,4}	t_0,3{3,3,4}	t_1,2{3,3,4}	t_0,1,2{3,3,4}	t_0,1,3{3,3,4}	t_0,1,2,3{3,3,4}
Schlegel diagram
B₄ Coxeter plane graph

Notes

^ Klitizing, (o3o3o4o - tat)
^ Klitizing, (o3x3x4o - tah)
^ Klitizing, (x3x3o4o - thex)

References

T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
H.S.M. Coxeter:
- Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973, p.296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  - (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  - (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  - (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26. pp. 409: Hemicubes: 1_n1)
Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
2. Convex uniform polychora based on the tesseract (8-cell) and hexadecachoron (16-cell) - Models 13, 16, 17, George Olshevsky.
Richard Klitzing, 4D, uniform polytopes (polychora) o3o3o4o - tat, o3x3x4o - tah, x3x3o4o - thex

External links

Paper model of truncated tesseract created using nets generated by Stella4D software


Family	A_n	BC_n	D_n	E₆ / E₇ / E₈ / F₄ / G₂	H_n
Regular polygon	Triangle	Square		Hexagon	Pentagon
Uniform polyhedron	Tetrahedron	Octahedron • Cube	Demicube		Dodecahedron • Icosahedron
Uniform polychoron	5-cell	16-cell • Tesseract	Demitesseract	24-cell	120-cell • 600-cell
Uniform 5-polytope	5-simplex	5-orthoplex • 5-cube	5-demicube
Uniform 6-polytope	6-simplex	6-orthoplex • 6-cube	6-demicube	1₂₂ • 2₂₁
Uniform 7-polytope	7-simplex	7-orthoplex • 7-cube	7-demicube	1₃₂ • 2₃₁ • 3₂₁
Uniform 8-polytope	8-simplex	8-orthoplex • 8-cube	8-demicube	1₄₂ • 2₄₁ • 4₂₁
Uniform 9-polytope	9-simplex	9-orthoplex • 9-cube	9-demicube
Uniform 10-polytope	10-simplex	10-orthoplex • 10-cube	10-demicube
n-polytopes	n-simplex	n-orthoplex • n-cube	n-demicube	1_k2 • 2_k1 • k₂₁	pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes

Truncated tesseract

Contents